Edit #3: Sorry zunächst mal für den anfangs schlecht leserlichen Beitrag mit vielen Tippfehler (war gestern irgendwie nicht mein Tag - hatte so viel Mails schreiben müssen, dass am Abend einfach die Konzentration nachließ). Den Beitrag habe ich nochmal in Punkto Lesbarkeit überarbeitet und an einigen Stellen ergänzt und präzisiert.
@VJoe2max
Damit, dass die Temperaturdifferenz immer kleiner wird, war natürlich die Temperaturdifferenz zwischen Wasser und Luft gemeint. Und da die Temperatur des Wassers immer weiter über die Länge der durchflossenden Strecke kleiner wird, wird auch die Temperaturdifferenz zwischen Luft und Wasser kleiner. Das heist, bei 20°C Raumtemperaur, kann bei zwei baugleichen Radiatoren, der Radiator, welcher mit einer höheren Einströmtemperatur des Fluids beaufschlagt wird, einen größeren Wärmestrom abgeben, als der, welcher mit einer niedrigeren Einströmtemperatur des Fluids beaufschlagt wird. Einfach weil die Temperaturdifferenz zwischen Luft und Wasser größer ist.
Wie ich oben bereits geschrieben habe, gleicht sich das über die gesamte Radiatorfläche vollständig aus. Du musst den Wärmestrom vom Wasser an die Luft über die gesamte aktive Fläche integrieren

. Relevant für den algebraischen Ansatz ist daher die mittlere Wassertemperatur. Wie hoch das ΔT des Wassers ist spielt dabei keine Rolle. Ich versuche es mal anschaulicher zu erklären:
Mal angenommen du hättest einen sehr geringen Volumenstrom und auch noch eine recht hohe Heizleistung im Kreislauf, so dass das die Temperaturdifferenz des Wassers in einem sauber messbaren Bereich liegt - sagen wir 10K. Nun hättest du also direkt am Einlass eine hohe Wassertemperatur von, sagen wir 40°C, gegenüber einer Lufttemperatur von, sagen wir 20°C, und am Auslass eine Wassertemperatur von 30°C gegenüber derselben Lufttemperatur. Das lokale ΔT-Wasser-Luft beträgt also am Einlass 20K und am Auslass 10K. Der Radiator überträgt jedoch an jeder Stelle Wärme an die Luft. Die mittlere Wassertemperatur im Radiator beträgt dementsprechend 35°C und das mittlere ΔT-Wasser-Luft dementsprechend 15K. Der Wärmestrom vom Wasser an die Luft entspricht darüber hinaus im quasistationären Zustand (also bei konstanter Heizleitung bis das System thermisch stabil ist) stets exakt der eingespeisten Heizleistung.
Nimmst du nun den gleichen Kreislauf und den gleichen Radiator, gibst aber der Pumpe etwas mehr Power, so dass der Durchfluss steigt, ergibt sich aufgrund des höheren Volumenstroms eine geringere Temperaturdifferenz des Wassers zwischen Ein- und Auslass. Die Formel die du weiter unten genannt hast ist für den Wasserkreislauf richtig und umgestellt nach dem ΔT kannst du dir damit auch ausrechnen, dass sich bei gleicher Heizleistung (≡ Wärmestrom) z.B. eine Durchflussverdopplung in einer Halbierung des ΔT äußert. Sagen wir also wir verdoppeln den Durchfluss und haben nun statt 10K nur noch 5K Temperaturdifferenz des Wassers zwischen Ein- und Auslass. Auch jetzt wird im quasistationären Zustand nach wie vor die gleiche Wärmemenge vom Wasser an die Luft übertragen. Allerdings haben wir nun am Einlass nur noch eine Wassertemperatur von 37,5°C, was dort ein ΔT-Wasser-Luft von 17,5K ergibt, und am Auslass eine Wassertemperatur von 32,5°C, was dort einem ΔT-Wasser-Luft von 12,5K entspricht. Aufintegriert über die Fläche beträgt die Mitteltemperatur des Wasser im Radiator auch jetzt 35°C und das mittlere ΔT-Wasser-Luft liegt somit, genau wie im ersten Gedankenexperiment, weiterhin bei 15K. Dementsprechend ist über die gesamte Fläche des Radiators keine Änderung des Temperaturniveaus zu verzeichnen. Die Wärmeabgabe ändert sich im quasistationären Fall ohnehin nicht.
--
Edit zur Ergänzung: Das mittlere Temperaturniveau des Wassers und damit auch die Kühlperformance würde sich nur ändern, wenn man den Radiator besser belüftet, die einströmende Lufttemperatur senkt, oder eben die aktive Fläche erhöht. An den Parametern der Wasserseite kann man hingegen sehr lange drehen bis da irgendetwas messbar tun würde, denn sie ist letztlich aufgrund des großen Unterschieds in der spezifischen Wärmekapazität der beiden Medien zwischen denen die Wärme getauscht wird, für die Wärmeabgabe nahezu völlig irrelevant. Bei Wakü-Radiatoren ist stets die Luftseite limitierend und ist, aufgrund der oben erklärten Zusammenhänge, so gut wie unabhängig von der Temperaturspreizung des Wassers, maßgeblich für das erreichbare Temperaturniveau der Wasserseite verantwortlich.
Die Höhe des mittleren ΔT-Wasser-Luft ist in der Praxis näherungsweise nur noch von der Radiatorfläche abhängig, wenn ansonsten alle Parametern gleich bleiben. Verdoppelt man die aktive Fläche, halbiert sich in erster Näherung das ΔT-Wasser-Luft und halbiert man die Radiatorfläche, verdoppelt sich in etwa das ΔT-Wasser-Luft. Bei unendlicher Fläche geht das ΔT-Wasser-Luft theoretisch gegen Null. In der Praxis sind die erreichbaren Verkleinerungen des ΔT-Wasser-Luft verhältnismäßig schnell so gering, dass eine weitere massive Flächenvergrößerung sich in der Regel nicht mehr lohnt.
--
An der Temperaturdifferenz des Wassers im Kreislauf ändert die Fläche jedoch zunächst mal gar nichts. Nun könnte man, wie du ja bereits erwähnt hast, natürlich anführen, dass ein zweiter Radiator den Strömungswiderstand des Wassers etwas erhöht, was den Durchfluss etwas senkt, was wiederum die Temperaturdifferenz im Wasser leicht ansteigen lässt. Wenn du dir aber mit der selbst genannten Formel mal die Mühe machst auszurechnen, welche Größenordnung an Volumenstromänderung du ausgehend von den geringen realen Werten aus der Praxis brauchst, um hier eine nennenswerte Änderung zu bewirken, und des Weiteren den Strömungswiderstand eines Radiators im Vergleich zu Kühlern und anderen wesentlich restriktiveren Komponenten im Kreislauf ins Kalkül ziehst, wird dir schnell klar, dass das kein Argument ist was in der Praxis messbare Auswirkungen hätte. Es ist in der Tat so, dass bereits ab relativ geringer Volumenströme, bei den üblicherweise in Waküs transportierten Wärmeströmen, nur sehr geringe Temperaturdifferenzen im Wasserkreislauf auftreten, die in vielen Fällen sogar so klein sind, dass sie zumindest innerhalb der absoluten Messgenauigkeit der üblichen Sensorik liegen, so dass sich auch das gemessene Delta in der Überschneidung der Fehlerbalken befindet und somit nicht mehr sauber messbar ist.
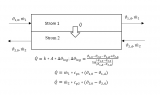
Die Temperaturdifferenz des Wassers zwischen Ein- und Auslass ist vernachlässigbar klein? Du weist ja das [Wärmestrom]=[Massenstrom Wasser]*[Wärmekapazität]*[Temperaturdifferenz] ist?
Glaub mir - ich bin der Letzte der diese Formel nicht kennt - schließlich dürfte ich einer derjenigen User hier im Forum sein, der sie am häufigsten anbringt und Ihre Aussage unermüdlich Neulingen erklärt

. Dieses Bild ist nicht umsonst eines, welches ich mit am häufigsten poste, wenn ich das Thema mal wieder erklären muss:

Ich fürchte allerdings, dass du sie etwas missverstanden hast, denn in dieser Formel steckt in unserem betrachteten Falle nicht das ΔT-Wasser-Luft, sondern die Temperaturdifferenz auf die Wasserseite, also das ΔT zwischen Ein- und Auslass des Radiators (man könnte sie auch auf die Luftseite anwenden - dann natürlich mit dem Massenstrom Luft und der spez. Wärmekapazität der Luft). Über die Wärmeübertragung vom Wasser an die Luft sagt sie aber absolut nichts aus. Sie beschreibt nur, das was ich im oben genannten Beispiel bezüglich des Einflusses von Durchfluss (und/oder Heizleistung) auf die Temperaturdifferenz des Wassers erklärt habe. Die spezifische Wärmekapazität ist im Temperaturbereich in dem Wasser flüssig ist übrigens als quasi konstant zu betrachten. Zwar hat sie eine gewisse Temperaturabhängigkeit, aber diese liegt bei Wasser unter 1% ihres Absolutwerts. Sie ist eine Stoffeigenschaft des strömenden Mediums.
Das ΔT der Wassers zwischen Einlauf und Auslauf eines Radiators hängt wohl von einigen Größen ab. Der Wärmeübertragerfläche, die Geschwindigkeit der Flüssigkeit->Wärmeübergangskoeffizient Flüssigkeit, Geschwindigkeit Luft->Wärmeübergangskoeffizient Luft. Prinzipiell auch von der Wärmeleitfähigkeit des Radiatorwerkstoffes. Variierbar ist bei einem gekauften Radiator natürlich nur der Luftmassenstrom, der Wassermassenstrom (und die Einflusstemperatur). Die Umgebungstemperatur ist ja meist vorgegeben. Nach diesen Größen stellt sich dann die Austrittstemperatur ein. Für die Berechnung des Wärmestroms eines Wärmeübertragers in Gegen oder Gleichstromschaltung nutzt man die mittlere logarithmische Temperaturdifferenz. So müssen nur die Ein- und Ausströmtemperaturen, sowie die Fläche und der Wärmedurchgangskoeffizient des Wärmeübertragers bekannt sein, um den Wärmestrom berechnen zu können. Da es sich bei den Radiatoren zumeist um Wärmetauscher der Art 'Kreuzstrom mit zwei Rohrreihen und zwei Durchgängen' handelt, kannst du ja mal im VDI-Wärmeatlas nachschauen wie 'simpel' es doch bei diesen ist.
Die von dir zitierte Formel gilt wie gesagt nur entweder für die Wasserseite oder für die Luftseite. All die Faktoren sie du nennst sind in der Tat wichtig für die Wärmeübertragung zwischen den Medien und damit für die Absoluttemperaturen die sich einstellen, aber eben keineswegs für die Temperaturdifferenzen
im Kreislauf

. Auf die mittlere Wassertemperatur und damit auch auf das konkrete ΔT-Wasser-Luft eines bestimmten Kreislaufs haben diese Faktoren aber selbstverständlich Einfluss. Bezüglich all dieser Einflussfaktoren kommt - wenn es denn so ausgeprägte Unterschiede gäbe - z. B. die thermische und strömungsmechanische Qualität und auch die Bauart der eingesetzten Radiatoren zum Tragen. In der Praxis kommen im Wakü-Bereich jedoch fast ausschließlich Querstromradiatoren sehr ähnlicher Bauart und meist auch mit einer recht geringen Bandbreite an Ausführungsvarianten und Materialien vor.
Du musst mir im Übrigen auch nicht erklären wie die verschiedenen Wärmetauschertypen funktionieren und auch nicht wie man sie berechnet - das mache ich beruflich oft genug

. Was ich jedoch oben dargestellt habe, ist, was die Wasserseite betrifft, in der Tat genau so simpel zu berechnen wie ich es im Beispiel getan habe und unter den genannten Randbedingungen ist auch das reziproke Verhältnis von Fläche und ΔT-Wasser-Luft, wenigstens in erster Näherung ebenso einfach. Da du ja offensichtlich ebenfalls Zugang zur einschlägigen Fachliteratur hast, kannst du dich ja noch mal etwas kundig machen, aber viel hilft hier auch praktische Erfahrung im Wakü-Bereich, denn dann engt sich der Parameterbereich in dem man überhaupt operieren kann so stark ein, so dass viele Faktoren kaum noch Relevanz haben. Der Knackpunkt ist meiner Ansicht nach wie gesagt deine falsche Annahme, dass es sich bei der Temperaturdifferenz im Wasser Einfluss auf die Temperaturdifferenz zwischen Wasser und Luft hätte - oder habe ich dich da falsch verstanden? Jedenfalls überträgt ein Radiator die eingespeiste Wärme über seine gesamte Fläche unabhängig von der lokalen Temperaturdifferenz an das andere Medium. Welche mittlere Absoluttemperatur sich dabei einstellt ist zwar in der Tat nicht einfach zu berechnen, aber wie sich eine Flächenänderung unter Beibehaltung aller anderen Einflussfaktoren auf die Temperaturdifferenz zwischen dieser Absoluttemperatur und der Raumtemperatur auswirkt, ist zumindest näherungsweise durchaus ein ähnlich linearer Zusammenhang wie der zwischen Volumenstrom und Temperaturdifferenz im Kreislauf.
Für die Auslegung von Wärmetauschern gelten selbstverständlich all die von dir angeführten Faktoren, weshalb man hier in der Tat nicht ohne Weiteres mal eben berechnen kann, wie hoch das konkrete ΔT-Wasser-Luft einem Radiators X bei Lüfterdrehzahl Y und abzuführender Heizleistung Z ist. Deshalb habe ich im obigen Beispiel auch nur Annahmen bezüglich der Absoluttemperaturen und damit des ΔT-Wasser-Luft (freilich in realistischen Größenordnungen) gemacht, denn das ist in der Tat von vielen, auch teilweise nichtlinearen Faktoren abhängig. Das gilt im Übrigen aber nicht nur für das ΔT-Wasser-Luft am Radiator, sondern natürlich auch für das ΔT-CPU-Wasser an den Kühlern. Beide Temperaturdifferenzen hängen u. A. z. B. auch von den absoluten Wärmewiderständen, von den Wärmeübergangskoeffizienten usw. ab, die ihrerseits z. B. wiederum stark vo Material und Konstruktion oder von fluiddynamischen Größen wie dem Turbulenzgrad abhängen. Bei Wakü-Radiatoren ist speziell der letztgenannte Faktor auf der Wasserseite jedoch in der Praxis vor allem aufgrund des großen Unterschieds der spezifischen Wärmekapazität zwischen Wasser und Luft bei gleichzeitig verhältnismäßig geringen Wärmeströmen und Temperaturdifferenzen ziemlich vernachlässigbar. Die Luftseite dominiert hier maßgeblich und gibt die Effektivität des Wärmeaustauschs vor.
VJoe2max schrieb:
Unter der Voraussetzung von Radiatoren gleicher Bauart und gleicher Lüfterdrehzahlen halbiert sich das ΔT zwischen Wasser und Luft, wenn die Lufteintrittfläche verdoppelt wird.'
Wären Wärmeübertrager so einfach zu berechnen, dann wären nicht ganze Bücher darüber verfasst worden.
Unter den genannten Voraussetzungen ist es im üblichen Genauigkeitsrahmen tatsächlich so einfach, denn so werden alle Parameter außer der Fläche festgehalten und das Problem wird zumindest unter dem Gesichtspunkt der Temperaturdifferenz linear

. Nimmst du unterschiedliche Radiatoren und änderst die Belüftung schaut die Sache freilich ein wenig anders aus. In erster Näherung haut es aber in der Praxis sogar in solchen Fällen ganz gut hin, wenn man nicht gerade an allen Stellschrauben massiv dreht, weil die Effektivität der Querstromradiatoren, die im Wakü-Bereich üblich sind, sich allgemein nicht so drastisch unterscheidet

. Das ist eben der Punkt an dem man auch ein bisschen Erfahrungswerte braucht, weil man hier mit reiner Theorie schnell mal in den Wald kommt, wenn man die tatsächlichen Spielräume aus der Praxis nicht kennt.
Edit#2: Hoffe ich habe die wichtigsten Punkte zu dem Thema erschlagen. Natürlich könne man jetzt noch ins Details gehen, was die Effektivität unterschiedlicher Radiatordicken und Lamellendichten bei Querstromradiatoren angeht usw., aber zum Einen habe ich das hier im Forum schön öfters ausführlich erklärt, und zum Anderen ist es nicht der Rede wert, sofern nicht geplant ist in nennenswertem Umfang mit den Lüfterdrehzahlen zu spielen. Bei Querstromradiatoren gilt allgemein: Lufteintrittsfläche schlägt Tiefe und wer´s leise aber dennoch effektiv haben will, bleibt besser bei schlanken Radiatoren mit möglichst viel Lufteintrittsfläche.

 Der Unterschied ist ein 120er Radiator, der kostet dich von Magicool um die 30€.
Der Unterschied ist ein 120er Radiator, der kostet dich von Magicool um die 30€.  Da würd ich lieber den zusätzlich nehmen.
Da würd ich lieber den zusätzlich nehmen.