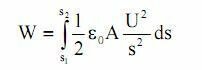Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.

Anmerkung: this_feature_currently_requires_accessing_site_using_safari
Du verwendest einen veralteten Browser. Es ist möglich, dass diese oder andere Websites nicht korrekt angezeigt werden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Der Hausaufgaben Thread(2)
- Ersteller dbode
- Erstellt am
- Status
- Für weitere Antworten geschlossen.
Ich suche ein paar Namen von den wichtigsten Gebieten großer Bodenerosionen, wie zum Beispiel der Great Plains.
http://de.wikipedia.org/wiki/Bodenerosion
hoi, ich hoffe der Link hilft. bei wiki gibts ne gute Karte von Südeuropa mit markierten Gebieten.
lg Akba
tigger
Semiprofi
- Mitglied seit
- 01.02.2004
- Beiträge
- 8.496
Ich brauch auch mal eure Hilfe.
Es geht um die Exponentialform einer komplexen Zahl.
Dazu habe ich folgende 2 Aufgaben, bei denen ich hänge
das was aussieht wie ein geschwungenes w soll der Winkel omega sein. Bei Wikipedia heißt er phi. j ist die imaginäre und e die eulersche Zahl. Der erste Ausdruck bei Aufgabe 1 ist 1 - e^(j * omega) und der zweite ist e^(j * (omega/2). Das bei Aufgabe 2 ist die Summe von n = 0 bis 7 von e^(j * omega * n) und man soll mit der endlichen geometr. Reihe diese Summe bestimmen. Habs etwas doof formuliert

Und hier meine Bearbeitung von Aufgabe 1. Kann man das noch weiter vereinfachen ?

zur 2. Aufgabe hab ich noch nix.
Es geht um die Exponentialform einer komplexen Zahl.
Dazu habe ich folgende 2 Aufgaben, bei denen ich hänge
das was aussieht wie ein geschwungenes w soll der Winkel omega sein. Bei Wikipedia heißt er phi. j ist die imaginäre und e die eulersche Zahl. Der erste Ausdruck bei Aufgabe 1 ist 1 - e^(j * omega) und der zweite ist e^(j * (omega/2). Das bei Aufgabe 2 ist die Summe von n = 0 bis 7 von e^(j * omega * n) und man soll mit der endlichen geometr. Reihe diese Summe bestimmen. Habs etwas doof formuliert


Und hier meine Bearbeitung von Aufgabe 1. Kann man das noch weiter vereinfachen ?

zur 2. Aufgabe hab ich noch nix.
Zuletzt bearbeitet:
- Mitglied seit
- 16.06.2005
- Beiträge
- 28.100
- Desktop System
- Cartman
- Details zu meinem Desktop
- Prozessor
- AMD Ryzen 9950x3D
- Mainboard
- ASUS ROG CROSSHAIR X870E APEX
- Kühler
- NZXT Kraken Z63
- Speicher
- G.Skill Trident Z5 RGB DDR5-6000 - 96GB - CL26
- Grafikprozessor
- Zotac GeForce RTX 5080
- Display
- Dell Alienware AW3423DW
- SSD
- Samsung 990 Pro 2TB + Samsung 970 Evo m2 1TB
- Gehäuse
- Jonsplus i400
- Netzteil
- be quiet! Straight Power 11
- Betriebssystem
- Microsoft Windows 11 Pro x64
- Webbrowser
- Firefox
- Sonstiges
- BambuLab X1C | Elegoo Mars 5 Ultra
- Internet
- ▼100 ▲40
- Mitglied seit
- 10.05.2006
- Beiträge
- 5.826
- Details zu meinem Desktop
- Prozessor
- Ryzen 7 5800X3D @90 W
- Kühler
- Noctua NH-D15 G2
- Speicher
- 32 GB DDR4
- Grafikprozessor
- PNY 3090 @3x Noctua NF-A9
- Display
- LG OLED42C29LB
- SSD
- Samsung 990 Pro 2TB || Evo 850 4TB || PM981a 1TB
- Soundkarte
- SoundBlaster X7 LE
- Gehäuse
- Jonsbo Z20W
- Netzteil
- Corsair SF750
- Keyboard
- Cherry KW X ULP
- Mouse
- Razer Viper Ultimate
- Sonstiges
- Audi e-tron GT
- Internet
- ▼100 ▲40
das Integral von 1/s² ist -1/s 

Ich hab ne ganz einfach Aufgabe und komm immer aufn falsches Ergebnis.
Wurzel von (2x² + 4x - 6) - x - 3 = 0 nach x auflösen. [Die Wurzel bezieht sich nur auf die Klammer]
Laut unserm Prof kommt da x1 = 5 und x2 = -3 raus. Ich wollte es mit der PQ-Formel machen aber irgendwas mach ich immer falsch
Wurzel von (2x² + 4x - 6) - x - 3 = 0 nach x auflösen. [Die Wurzel bezieht sich nur auf die Klammer]
Laut unserm Prof kommt da x1 = 5 und x2 = -3 raus. Ich wollte es mit der PQ-Formel machen aber irgendwas mach ich immer falsch

Desert Igel
Schanitzel König
@Tigger:
Wenn Du bei der ersten mit 2j erweiterst, kannst Du einen -Sinus aus der Klammer machen. In der letzten Zeile fehlt beim mittleren e^ das - im Exponent.
Die Zweite kannst du als (e^(..))^n umschreiben und kannst dann die geom. Summe darauf anwenden. Danach kannst Du den Zähler 2 oder 3 Mal mit der dritten binomischen Formel zerhacken, bis Du kürzen kannst.
Vielleicht ergibt sich danach was schönes
Wenn Du bei der ersten mit 2j erweiterst, kannst Du einen -Sinus aus der Klammer machen. In der letzten Zeile fehlt beim mittleren e^ das - im Exponent.
Die Zweite kannst du als (e^(..))^n umschreiben und kannst dann die geom. Summe darauf anwenden. Danach kannst Du den Zähler 2 oder 3 Mal mit der dritten binomischen Formel zerhacken, bis Du kürzen kannst.
Vielleicht ergibt sich danach was schönes

tigger
Semiprofi
- Mitglied seit
- 01.02.2004
- Beiträge
- 8.496
danke Igelchen, das mit dem -Sinus hab ich heute in der Übung auch gesehen 
Ich sollte mit den Übungen früher anfangen, die Aufgaben waren verschenkte Punkte.
@ bill
sorry, kann nix damit anfangen
@ krooms


Ich sollte mit den Übungen früher anfangen, die Aufgaben waren verschenkte Punkte.
@ bill
sorry, kann nix damit anfangen

@ krooms
Code:
Wurzel von (2x² + 4x - 6) - x - 3 = 0 | + x + 3
-> Wurzel von (2x² + 4x - 6) = x + 3 | Quadrat
-> 2x² + 4x - 6 = x² + 6x + 9 | - x² - 6x - 9
-> x² - 2x - 15
in der PQ Formel ergibt das
x_1/2 = 1 +- Wurzel von (1 + 15)
das ergibt x1 = 5 und x2 = -3
Zuletzt bearbeitet:
t0rben
Neuling
Moin,
ich muss ein Referate über Markenpiraterie im Zusammenhang mit Globalisierung anfertigen. Bis jetzt habe ich nur allgemeine Sachen, sprich Definition, ein paar Beispiele usw. Und jetzt stehe ich irgendwie auf dem Schlauch.
Könnt ihr mir vielleicht ein paar Tipps geben, was man noch so schreiben könnte ?
ich muss ein Referate über Markenpiraterie im Zusammenhang mit Globalisierung anfertigen. Bis jetzt habe ich nur allgemeine Sachen, sprich Definition, ein paar Beispiele usw. Und jetzt stehe ich irgendwie auf dem Schlauch.
Könnt ihr mir vielleicht ein paar Tipps geben, was man noch so schreiben könnte ?
Moin Leute, ich hab hier ne ganz einfache Aufgabe, ...
Eine Schnecke ist in einen 21m tiefen Brunnen gefallen, sie macht sich nun wieder an den Aufstieg. Sie schafft am Tag 7m, rutscht aber in der Nacht um 4m wieder zurück.
Wie viele Tage braucht die Schnecke um aus dem Brunnen zu kommen.
Das ist die Aufgabenstellung, mehr steht da nicht. Rein Mathematisch ist das ja ganz einfach, mal schaun was ihr da raus bekommt.
Zur Info schon mal vorweg, es sind nicht 7 Tage
Eine Schnecke ist in einen 21m tiefen Brunnen gefallen, sie macht sich nun wieder an den Aufstieg. Sie schafft am Tag 7m, rutscht aber in der Nacht um 4m wieder zurück.
Wie viele Tage braucht die Schnecke um aus dem Brunnen zu kommen.
Das ist die Aufgabenstellung, mehr steht da nicht. Rein Mathematisch ist das ja ganz einfach, mal schaun was ihr da raus bekommt.
Zur Info schon mal vorweg, es sind nicht 7 Tage

@Thomas92
Neja wenn man genau rechnet, brauch die Schnecke offiziell 5 Tage und 6/7 vom 6. Tag.
Das Problem was ich sehe, sind aber die, 6/7 vom 6. Tag.
Denn der Tag hat 24h, 6/7 von diesen 24h sind etwas über 20,5h.
Die Frage wäre jetzt, wann beginnt die Nacht und vor allem, wie lange geht für die Fragesteller ein Tag.
Denn wenn die Nacht vor ablauf der ca. 20,5h beginnt rutscht die Schnecke ja wiederum 4m zurück und müsste dann am nächsten Tag erst den Rand erreichen...
Neja wenn man genau rechnet, brauch die Schnecke offiziell 5 Tage und 6/7 vom 6. Tag.
Das Problem was ich sehe, sind aber die, 6/7 vom 6. Tag.
Denn der Tag hat 24h, 6/7 von diesen 24h sind etwas über 20,5h.
Die Frage wäre jetzt, wann beginnt die Nacht und vor allem, wie lange geht für die Fragesteller ein Tag.
Denn wenn die Nacht vor ablauf der ca. 20,5h beginnt rutscht die Schnecke ja wiederum 4m zurück und müsste dann am nächsten Tag erst den Rand erreichen...
Zuletzt bearbeitet:
- Mitglied seit
- 16.06.2005
- Beiträge
- 28.100
- Desktop System
- Cartman
- Details zu meinem Desktop
- Prozessor
- AMD Ryzen 9950x3D
- Mainboard
- ASUS ROG CROSSHAIR X870E APEX
- Kühler
- NZXT Kraken Z63
- Speicher
- G.Skill Trident Z5 RGB DDR5-6000 - 96GB - CL26
- Grafikprozessor
- Zotac GeForce RTX 5080
- Display
- Dell Alienware AW3423DW
- SSD
- Samsung 990 Pro 2TB + Samsung 970 Evo m2 1TB
- Gehäuse
- Jonsplus i400
- Netzteil
- be quiet! Straight Power 11
- Betriebssystem
- Microsoft Windows 11 Pro x64
- Webbrowser
- Firefox
- Sonstiges
- BambuLab X1C | Elegoo Mars 5 Ultra
- Internet
- ▼100 ▲40
@Thomas92
Neja wenn man genau rechnet, brauch die Schnecke offiziell 5 Tage und 6/7 vom 6. Tag.
Das Problem was ich sehe, sind aber die, 6/7 vom 6. Tag.
Denn der Tag hat 24h, 6/7 von diesen 24h sind etwas über 20,5h.
Die Frage wäre jetzt, wann beginnt die Nacht und vor allem, wie lange geht für die Fragesteller ein Tag.
Denn wenn die Nacht vor ablauf der ca. 20,5h beginnt rutscht die Schnecke ja wiederum 4m zurück und müsste dann am nächsten Tag erst den Rand erreichen...
ist doch egal
steht doch da das sie am tag 7 meter schaft, da ist doch egal wie lang der tag ist

bei 6 tagen (ohne zurückrutschen am letzten tag) kommt man auf 22 meter
somit wäre sie aus dem brunnen
eraser777
Urgestein
- Mitglied seit
- 22.01.2006
- Beiträge
- 2.780
Rechnet mir mal bitte wer die Formel der Regressionsgeraden für die Punkte
P1(2/1)
P2(1/2)
P3(4/4)
P4(1/1)
aus?
Die Punkte habe ich mir ausgedacht und es dient nur zur Übung. Wollte gucken ob meine Formel richtig ist (was ich nicht glaube, da sie über alle Punkte hinweg geht und den Schwerpunkt der Punkte S(2/2) nicht schneidet.)
Danke
P1(2/1)
P2(1/2)
P3(4/4)
P4(1/1)
aus?
Die Punkte habe ich mir ausgedacht und es dient nur zur Übung. Wollte gucken ob meine Formel richtig ist (was ich nicht glaube, da sie über alle Punkte hinweg geht und den Schwerpunkt der Punkte S(2/2) nicht schneidet.)

Danke
Zur Schneckenaufgabe: Sie braucht 5 Tage und 6/7 des 6ten Tages (das stimmt schon @fdsonne)! Und wie King Bill schon gesagt hat, die Länge des Tages ist egal.
Wir bezeichnen zwar im alltäglichen Sprachgebrauch 24 Stunden als einen Tag, hier sind die 24 Stunden aber in Tag und Nacht eingeteilt.
Egal, was wie lange dauert, die Nacht fängt erst an, wenn der Tag aufhört Also ist deine Überlegung, dass die Schnecke nochmal abrutschen könnte falsch.
Also ist deine Überlegung, dass die Schnecke nochmal abrutschen könnte falsch.
@socko: Was genau hast du denn schon alles an Beispielen und Defenitionen gebracht. Und worauf sollst du alles eingehen? Auf Möglichkeiten der Bekämpfung der Piraterie? Auf die Auswirkungen auf die Wirtschaft im Land wo geklaut wird und dort wo die kopierten Waren verkauft werden?
Wir bezeichnen zwar im alltäglichen Sprachgebrauch 24 Stunden als einen Tag, hier sind die 24 Stunden aber in Tag und Nacht eingeteilt.
Denn wenn die Nacht vor ablauf der ca. 20,5h beginnt rutscht die Schnecke ja wiederum 4m zurück [...]
Egal, was wie lange dauert, die Nacht fängt erst an, wenn der Tag aufhört
 Also ist deine Überlegung, dass die Schnecke nochmal abrutschen könnte falsch.
Also ist deine Überlegung, dass die Schnecke nochmal abrutschen könnte falsch.@socko: Was genau hast du denn schon alles an Beispielen und Defenitionen gebracht. Und worauf sollst du alles eingehen? Auf Möglichkeiten der Bekämpfung der Piraterie? Auf die Auswirkungen auf die Wirtschaft im Land wo geklaut wird und dort wo die kopierten Waren verkauft werden?
- Mitglied seit
- 10.05.2006
- Beiträge
- 5.826
- Details zu meinem Desktop
- Prozessor
- Ryzen 7 5800X3D @90 W
- Kühler
- Noctua NH-D15 G2
- Speicher
- 32 GB DDR4
- Grafikprozessor
- PNY 3090 @3x Noctua NF-A9
- Display
- LG OLED42C29LB
- SSD
- Samsung 990 Pro 2TB || Evo 850 4TB || PM981a 1TB
- Soundkarte
- SoundBlaster X7 LE
- Gehäuse
- Jonsbo Z20W
- Netzteil
- Corsair SF750
- Keyboard
- Cherry KW X ULP
- Mouse
- Razer Viper Ultimate
- Sonstiges
- Audi e-tron GT
- Internet
- ▼100 ▲40
@kommando: hast du net noch was vergessen?
s^-2 wird doch zu (s^-1)/-2
kombiniert mit den 1/2 dies schon hat wirds dann -4 im nenner
==>attachment
d/ds(1/s²) = -2/s³, aber "integral"(1/s²)ds = -1/s

fast forward
Enthusiast
brauch auch mal hilfe
komme gerade nicht weiter.
4 cos (3x) -1 = 0 -> cos (3x) = 1 / 4 ; ja was nun?
cos (3x) kann ich auch in cos^3 x * 3cos x umwandeln, aber das bringt mir auch nichts.
ich soll alle x werte im intervall 0 - 2pi errechnen.
cos und einfach bei +- y = 0.439 eine gerade ziehen, dann sieht man die "schnittpunkte" (gerade/cosinus)
noch ne grafik, damit es leichter zu verstehen ist.

1. Semester Mathematik I (FH)
komme gerade nicht weiter.
4 cos (3x) -1 = 0 -> cos (3x) = 1 / 4 ; ja was nun?
cos (3x) kann ich auch in cos^3 x * 3cos x umwandeln, aber das bringt mir auch nichts.
ich soll alle x werte im intervall 0 - 2pi errechnen.
cos und einfach bei +- y = 0.439 eine gerade ziehen, dann sieht man die "schnittpunkte" (gerade/cosinus)
noch ne grafik, damit es leichter zu verstehen ist.

1. Semester Mathematik I (FH)
TheWarrior
Enthusiast
- Mitglied seit
- 15.11.2003
- Beiträge
- 384
3x = acos(1/4), x = acos(1/4)/3.4 cos (3x) -1 = 0 -> cos (3x) = 1 / 4 ; ja was nun?
dann musst du dir nur noch überlegen, wo sich die werte in deinem intervall wiederholen
fast forward
Enthusiast
menno, das war ja einfach. Habe nicht an die Umkehrfunktion gedacht, da wir es vorher anders gemacht haben.
Danke
x1 = 0.493 x2 = 1.665 x3 = 2.543 x4 = 3.794 x5 = 4.628 x6 = 5.844
tada
Danke
x1 = 0.493 x2 = 1.665 x3 = 2.543 x4 = 3.794 x5 = 4.628 x6 = 5.844
tada
Zuletzt bearbeitet:
fast forward
Enthusiast
Habe eine Physikaufgabe, die ich nicht hinbekomme:
Ein Stein fällt in einem Brunnen, seine Anfangsgeschwindigkeit ist 0 m/s. Nach 1,7 s
wird ein zweiter Stein mit der Anfangsgeschwindigkeit von 25 m/s nachgeworfen. Der
Luftwiderstand soll nicht berücksichtigt werden.
a. Welche Zeit vergeht nach dem Start des ersten Steines, bis dieser vom Zweiten überholt
wird?
b. In welcher Tiefe findet dieser Überholvorgang statt?
Ein Stein fällt in einem Brunnen, seine Anfangsgeschwindigkeit ist 0 m/s. Nach 1,7 s
wird ein zweiter Stein mit der Anfangsgeschwindigkeit von 25 m/s nachgeworfen. Der
Luftwiderstand soll nicht berücksichtigt werden.
a. Welche Zeit vergeht nach dem Start des ersten Steines, bis dieser vom Zweiten überholt
wird?
b. In welcher Tiefe findet dieser Überholvorgang statt?
TheWarrior
Enthusiast
- Mitglied seit
- 15.11.2003
- Beiträge
- 384
Deine Steine werden mit g=9.81m/s^2 beschleunigt. Stein 1 hat eine Anfangsgeschwindigkeit 0m/s, hat zur Zeit t also die Geschwindigkeit t*g.
Für den zweiten Stein bekommst du die Geschwindigkeit 25m/s+(t-1.7s)*g.
Jetzt kannst du das gleichsetzen, und kriegst die Zeit, wann sie gleichschnell sind.
Diese Zeit setzt du in die Formel für den freien Fall ein und kennst die Tiefe.
Für den zweiten Stein bekommst du die Geschwindigkeit 25m/s+(t-1.7s)*g.
Jetzt kannst du das gleichsetzen, und kriegst die Zeit, wann sie gleichschnell sind.
Diese Zeit setzt du in die Formel für den freien Fall ein und kennst die Tiefe.
fast forward
Enthusiast
Deine Steine werden mit g=9.81m/s^2 beschleunigt. Stein 1 hat eine Anfangsgeschwindigkeit 0m/s, hat zur Zeit t also die Geschwindigkeit t*g.
Für den zweiten Stein bekommst du die Geschwindigkeit 25m/s+(t-1.7s)*g.
Jetzt kannst du das gleichsetzen, und kriegst die Zeit, wann sie gleichschnell sind.
Diese Zeit setzt du in die Formel für den freien Fall ein und kennst die Tiefe.
ahhh danke!!

sapphire_pro
Enthusiast
- Mitglied seit
- 18.10.2004
- Beiträge
- 7.930
Physikexperiement Kondensatorentladung: Brauche Hilfe beim Erstellen der Gleichungen
Hallo liebes Forum,
ich habe ein dickes Problem in Physik. Ich soll für nächste Woche ein Experiment vorbereiten (Kondensatorentladung) aber leider habe ich von diesem Themengebiet keine Ahnung.
Es geht im Prinzip um die Vorbetrachtung des Experiments.
Folgende Aufgaben kann ich nicht lösen:
1. Man kann Imax mit Hilfe der Ladespannung U genauer bestimmen. Geben sie dafür eine Gleichung an!
2. Die Ladung des Kondensators kann auch mit Hilfe der Kapazität und der anliegenden Höchstspannung berechnet werden. Geben sie eine Gleichung dafür an!
Ich hoffe es kann mir jemand helfen.
Hallo liebes Forum,
ich habe ein dickes Problem in Physik. Ich soll für nächste Woche ein Experiment vorbereiten (Kondensatorentladung) aber leider habe ich von diesem Themengebiet keine Ahnung.
Es geht im Prinzip um die Vorbetrachtung des Experiments.
Folgende Aufgaben kann ich nicht lösen:
1. Man kann Imax mit Hilfe der Ladespannung U genauer bestimmen. Geben sie dafür eine Gleichung an!
2. Die Ladung des Kondensators kann auch mit Hilfe der Kapazität und der anliegenden Höchstspannung berechnet werden. Geben sie eine Gleichung dafür an!
Ich hoffe es kann mir jemand helfen.
Reden wir vom Wechselstromkreis? Wenn ja, dann kann man bei 1. Imax durch Umax und X (Blindwiderstand des Kondensators) bestimmen:
I = U/R
Wenn es um den Wechselstromkreis geht, dann ist das mit I schwieriger. Du kannst nur ja I immer nur zur aktuellen Zeit bestimmen. Und zwar indem du weißt, wie sich die Ladung Q in der Zeit t verändert hat. Die Formel hierfür wäre:
I= dQ/dt
zu 2.
C = Q/U ergibt umgestellt Q = C*U das dürfte deine Frage beantworten.
I = U/R
Wenn es um den Wechselstromkreis geht, dann ist das mit I schwieriger. Du kannst nur ja I immer nur zur aktuellen Zeit bestimmen. Und zwar indem du weißt, wie sich die Ladung Q in der Zeit t verändert hat. Die Formel hierfür wäre:
I= dQ/dt
zu 2.
C = Q/U ergibt umgestellt Q = C*U das dürfte deine Frage beantworten.
Real ACC
Semiprofi
Hallo, ich soll das Rotationsvolumen der Kugel errechnen. Ich bin jetzt beim einsetzen der Grenzen angelangt (allgemeine Formel, Intervall [0;r] )
Also: 2(PI) [r²-1/3 r³ - 0]
Wie geht es jetzt weiter? 4/3(PI) r³ muss ja rauskommen...
Also: 2(PI) [r²-1/3 r³ - 0]
Wie geht es jetzt weiter? 4/3(PI) r³ muss ja rauskommen...
TheWarrior
Enthusiast
- Mitglied seit
- 15.11.2003
- Beiträge
- 384
Fehlt da nicht noch deine Integrationsvariable in der Klammer?
PoWerBaR
Semiprofi
@tetra: Bei dir müsste das erste Wechselstromkreis wohl eher Gleichstromkreis heißen, gibt sonst keinen Sinn.
@sapphire_pro: Dafür gibt nen extra Hausaufgabenthread! Bitte da reinschreiben. Desweiteren bekommst du die Lösungen mit paar Sekunden googeln raus.
@sapphire_pro: Dafür gibt nen extra Hausaufgabenthread! Bitte da reinschreiben. Desweiteren bekommst du die Lösungen mit paar Sekunden googeln raus.
- Status
- Für weitere Antworten geschlossen.
Ähnliche Themen
- Antworten
- 0
- Aufrufe
- 842
- Antworten
- 1
- Aufrufe
- 537
- Antworten
- 9
- Aufrufe
- 714