Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.

Anmerkung: this_feature_currently_requires_accessing_site_using_safari
Du verwendest einen veralteten Browser. Es ist möglich, dass diese oder andere Websites nicht korrekt angezeigt werden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Der Hausaufgaben Thread
- Ersteller dbode
- Erstellt am
Autokiller677
Semiprofi
- Mitglied seit
- 09.06.2009
- Beiträge
- 1.161
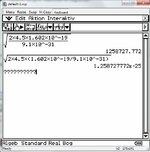
Ach, sry, ich hab eben im Kopf auch etwas Murks gemacht. Beim wegkürzen bleiben im Nenner ^-12 stehen, wenn man die dann in den Zähler holt werden daraus ^12. Wenn man dann die Wurzel zieht, kommen die 1,258*10^6 raus. Bist du sicher, dass in der Lösung -6 steht?
Bei deiner 2. Rechnung fehlt eine Klammer um den Nenner, so teilt er nur durch 9,1 und multipliziert den ganzen Bruch mit ^-31
Bei deiner 2. Rechnung fehlt eine Klammer um den Nenner, so teilt er nur durch 9,1 und multipliziert den ganzen Bruch mit ^-31
Zuletzt bearbeitet:
SturmGhost
Enthusiast
Argh und ich kann nicht lesen... ja Sie schreiben 10^6... Ich weiß aber immer noch nicht warum der TA daraus -25 bastelt...
Autokiller677
Semiprofi
- Mitglied seit
- 09.06.2009
- Beiträge
- 1.161
Er multipliziert jetzt ja die ^-19 mit den ^-31.
Potenzen werden potenziert indem man die Exponenten addiert, also -19+-31=-50
sqrt(^-50)=^-50^0,5=^-50*0,5=^-25
Potenzen werden potenziert indem man die Exponenten addiert, also -19+-31=-50
sqrt(^-50)=^-50^0,5=^-50*0,5=^-25
Zuletzt bearbeitet:
Autokiller677
Semiprofi
- Mitglied seit
- 09.06.2009
- Beiträge
- 1.161
Ich brauch mal kurz eure Hilfe.
Ich habe die Gleichung: 480e^(ka)-e^(2ka)=43.200
k ist ein Parameter, a die Variable, nach der auch aufgelöst werden soll.
Ergebnis ist a=ln(120)/k.
Aber irgendwie komm ich so gar nicht weiter. Wenn ich ln anwende, hab ich auf der linken Seite immer eine Differenz im ln stehen, bei der ich dann hängen bleibe.
Edit: Bin doch auf die Lösung gekommen. Einfach eine quadratische Erweiterung machen und schon hat man ein schönes Ergebnis.
Ich habe die Gleichung: 480e^(ka)-e^(2ka)=43.200
k ist ein Parameter, a die Variable, nach der auch aufgelöst werden soll.
Ergebnis ist a=ln(120)/k.
Aber irgendwie komm ich so gar nicht weiter. Wenn ich ln anwende, hab ich auf der linken Seite immer eine Differenz im ln stehen, bei der ich dann hängen bleibe.
Edit: Bin doch auf die Lösung gekommen. Einfach eine quadratische Erweiterung machen und schon hat man ein schönes Ergebnis.
Zuletzt bearbeitet:
SturmGhost
Enthusiast
Autokiller677
Semiprofi
- Mitglied seit
- 09.06.2009
- Beiträge
- 1.161
Bei der 2. partiellen Integration muss vor den Integral ein +, weil bei der 1. ein Minus davorstand. -*- ist ja bekanntlich +.
Zuletzt bearbeitet:
SturmGhost
Enthusiast
Dann bekomme ich aber beim einsetzen der ersten Grenze (-3) -> -2*e^-3 +6 raus und bei der zweiten Grenze 1... Das ergibt aber keine -4*e^-3+1
fl0
Enthusiast
G
Gelöschtes Mitglied 4152
Guest
Wer es noch nicht kennt:
wolfram alpha
Kann alles rechnen, mit Schritt für Schritt-Erklärung.
wolfram alpha
Kann alles rechnen, mit Schritt für Schritt-Erklärung.
fl0
Enthusiast
^^alles nicht  aber viele sachen schon, das stimmt. vor allem mit matrizen kann man da nicht viel machen, davon abgesehen dass die rechnung per hand bei kleinen matrizen schneller geht als das umständlich eintippen
aber viele sachen schon, das stimmt. vor allem mit matrizen kann man da nicht viel machen, davon abgesehen dass die rechnung per hand bei kleinen matrizen schneller geht als das umständlich eintippen 
 aber viele sachen schon, das stimmt. vor allem mit matrizen kann man da nicht viel machen, davon abgesehen dass die rechnung per hand bei kleinen matrizen schneller geht als das umständlich eintippen
aber viele sachen schon, das stimmt. vor allem mit matrizen kann man da nicht viel machen, davon abgesehen dass die rechnung per hand bei kleinen matrizen schneller geht als das umständlich eintippen 
Autokiller677
Semiprofi
- Mitglied seit
- 09.06.2009
- Beiträge
- 1.161
Der hat schon ein paar Funktionen zu Matrizen, aber das eintippen ist halt ewig aufwendig. Da ist mein Taschenrechner besser ausgelegt.
@SturmGhost: Ich sehe gerade, dass die 2. Integration auch gar nicht nötig ist. 2x+4e^x sind einfach 0,5*2*x²+4e^x. Hier ist das Kriterium ja nicht erfüllt: Es sind keine 2 verschiedenen Funktionstypen mehr über * verknüpft. Man kann einen Integral auch einfach auf jeden Summanden einzeln Verteilen, also statt S(2x+4e^x) kann man S(2x)+S(4e^x) machen. Die kann man so ohne Trick und doppelten Boden einfach wegintegrieren.
Wie gesagt: Solange verschiedene Funktionstypen nicht über * verknüpft sind, kann man einfach jeden Summanden für sich addieren.
@SturmGhost: Ich sehe gerade, dass die 2. Integration auch gar nicht nötig ist. 2x+4e^x sind einfach 0,5*2*x²+4e^x. Hier ist das Kriterium ja nicht erfüllt: Es sind keine 2 verschiedenen Funktionstypen mehr über * verknüpft. Man kann einen Integral auch einfach auf jeden Summanden einzeln Verteilen, also statt S(2x+4e^x) kann man S(2x)+S(4e^x) machen. Die kann man so ohne Trick und doppelten Boden einfach wegintegrieren.
Wie gesagt: Solange verschiedene Funktionstypen nicht über * verknüpft sind, kann man einfach jeden Summanden für sich addieren.
SturmGhost
Enthusiast
Der hat schon ein paar Funktionen zu Matrizen, aber das eintippen ist halt ewig aufwendig. Da ist mein Taschenrechner besser ausgelegt.
@SturmGhost: Ich sehe gerade, dass die 2. Integration auch gar nicht nötig ist. 2x+4e^x sind einfach 0,5*2*x²+4e^x. Hier ist das Kriterium ja nicht erfüllt: Es sind keine 2 verschiedenen Funktionstypen mehr über * verknüpft.
Hö? Wie hast du das denn nun gemacht? Also hätte ich nach der zweiten Zeile auf dem Blatt aufhören können und einfach das Integral 2x+4*e^x ausrechnen können?
Das mit den verschiedenen Funktionstypen verstehe ich immer noch nicht. Und wenn ich ehrlich bin, kann ich mit dem Begriff "Funktionstypen" jetzt nicht relativ viel anfangen. - Ich gebe auch zu nicht nach gesucht zu haben (Google).
Und streng genommen steht doch dort immer ein *, denn 2x ist mit einem * verbunden und die e^x ja eig. auch mit dem Rest vom Term (2x+4)...
Ich liebe dieses "auf den Taschenrechner dressieren und stur Befehle auswendig lernen ohne die Materie dahinter wirklich verstanden zu haben", um später in der Uni richtig ab zukacken weil dort Taschenrechner ein Fremdwort ist.

fl0
Enthusiast
jepp, autokiller hat sich vertan. da steht nämlich ne klammer (2x+4)e^x. ausserdem sieht man direkt am start schon dass man 2 mal partiell integrieren muss, schliesslich ist das polynom vom grad 2 und bis man da bei ner konstanten ankommt dauert es eben 2 ableitungen.
nochmal zu "verschiedenen" funktionen, in der mathematik nennt man etwas linear wenn gilt, dass f(a+b)=f(a)+f(b) ist. zb. ist eine parabel f(x)=x^2 nicht linear weil (a+b)^2 nicht immer das gleiche ist wie (a)^2+(b)^2. integrale sind aber linear, deswegen darfst du S(a+b) (S soll das integrationssymbol sein) auch einzeln integrieren, also S(a)+S(b). das gilt aber nur wenn du addierst, bei multiplikationen oder hintereinanderausführung geht die linearität verloren. für die multiplikation gibt es dann die partielle integration und für die hintereinandeausführung (also f(g(x)), erst wird g auf x angewendet und dann f) gibt es die substitution. hast du zb.
S cos(x) + x^2 als integral ist das linear, also S cos(x) + S(x^2), hast du S cos(x)*x^2 ist das quasi das selbe problem wie bei deiner aufgabe, weil die beiden "verschiedenen" funktionen mit * verknüpft sind und wenn du zb.
S cos(x^2) hättest, wäre das die hintereinanderausführung. bei "gleichen" funktionen ist es einfacher, polynome kannst du miteinander verrechnen und dann wieder einzeln jeden summand integrieren. potenzfunktionen ebenso, für trigonometrische funktionen gibts nen arsch voll identitäten die man mit glück ausnutzen kann und so weiter halt.
edit: und das bissle was wolfram alpha bei matrizen kann ist echt nicht wert den krempel einzutippen, finde ich zumindest. normen gehn nicht (oder ich check nicht wie ), eigenwerte nur bedingt wie mir vorkommt, irgendwelche zerlegungen ebenso nicht (oder ich kenne auch hier die befehle einfach nicht), die determinante kann ich selber ausrechnen
), eigenwerte nur bedingt wie mir vorkommt, irgendwelche zerlegungen ebenso nicht (oder ich kenne auch hier die befehle einfach nicht), die determinante kann ich selber ausrechnen  und zb. den cos(A) oder e^At oder ähnliches hab ich auch noch nie hinbekommen.
und zb. den cos(A) oder e^At oder ähnliches hab ich auch noch nie hinbekommen.
nochmal zu "verschiedenen" funktionen, in der mathematik nennt man etwas linear wenn gilt, dass f(a+b)=f(a)+f(b) ist. zb. ist eine parabel f(x)=x^2 nicht linear weil (a+b)^2 nicht immer das gleiche ist wie (a)^2+(b)^2. integrale sind aber linear, deswegen darfst du S(a+b) (S soll das integrationssymbol sein) auch einzeln integrieren, also S(a)+S(b). das gilt aber nur wenn du addierst, bei multiplikationen oder hintereinanderausführung geht die linearität verloren. für die multiplikation gibt es dann die partielle integration und für die hintereinandeausführung (also f(g(x)), erst wird g auf x angewendet und dann f) gibt es die substitution. hast du zb.
S cos(x) + x^2 als integral ist das linear, also S cos(x) + S(x^2), hast du S cos(x)*x^2 ist das quasi das selbe problem wie bei deiner aufgabe, weil die beiden "verschiedenen" funktionen mit * verknüpft sind und wenn du zb.
S cos(x^2) hättest, wäre das die hintereinanderausführung. bei "gleichen" funktionen ist es einfacher, polynome kannst du miteinander verrechnen und dann wieder einzeln jeden summand integrieren. potenzfunktionen ebenso, für trigonometrische funktionen gibts nen arsch voll identitäten die man mit glück ausnutzen kann und so weiter halt.
edit: und das bissle was wolfram alpha bei matrizen kann ist echt nicht wert den krempel einzutippen, finde ich zumindest. normen gehn nicht (oder ich check nicht wie
 ), eigenwerte nur bedingt wie mir vorkommt, irgendwelche zerlegungen ebenso nicht (oder ich kenne auch hier die befehle einfach nicht), die determinante kann ich selber ausrechnen
), eigenwerte nur bedingt wie mir vorkommt, irgendwelche zerlegungen ebenso nicht (oder ich kenne auch hier die befehle einfach nicht), die determinante kann ich selber ausrechnen  und zb. den cos(A) oder e^At oder ähnliches hab ich auch noch nie hinbekommen.
und zb. den cos(A) oder e^At oder ähnliches hab ich auch noch nie hinbekommen.
Zuletzt bearbeitet:
Autokiller677
Semiprofi
- Mitglied seit
- 09.06.2009
- Beiträge
- 1.161
Oh, tut mir leid. Ich hatte nicht jeden Schritt nachgerechnet und auf dem Blatt stands halt ohne Klammer, deshalb dachte ich das geht so^^.
SturmGhost
Enthusiast
Danke für die Erklärung. Die Aufgabe mit der partiellen Integration habe ich in der heutigen Klausur auch ganz easy geschafft. Dafür hat es dann bei anderen Sachen gehackt.  Ich finde es übrigens total super, wenn in Klausuren plötzlich Begriffe vorkommen, die man im Leben noch nicht gehört hat. Zum Beispiel so etwas wie "Achsendurchgangspunkt(e)"...
Ich finde es übrigens total super, wenn in Klausuren plötzlich Begriffe vorkommen, die man im Leben noch nicht gehört hat. Zum Beispiel so etwas wie "Achsendurchgangspunkt(e)"...
 Ich finde es übrigens total super, wenn in Klausuren plötzlich Begriffe vorkommen, die man im Leben noch nicht gehört hat. Zum Beispiel so etwas wie "Achsendurchgangspunkt(e)"...
Ich finde es übrigens total super, wenn in Klausuren plötzlich Begriffe vorkommen, die man im Leben noch nicht gehört hat. Zum Beispiel so etwas wie "Achsendurchgangspunkt(e)"...
Zuletzt bearbeitet:
normen gehn nicht (oder ich check nicht wie )
Eigentlich ganz intuitiv: ||A||
eigenwerte nur bedingt wie mir vorkommt
Gehen wohl. Sind nur grausam ungenau

irgendwelche zerlegungen ebenso nicht (oder ich kenne auch hier die befehle einfach nicht)
Gehen zumindest teilweise schon. Steht aber auch hier: Wolfram|Alpha Examples - Matrices & Linear Algebra
fl0
Enthusiast
geht nur die (ich vermute mal dass sie es ist) 2-norm?
den rest muss ich mir mal anschauen, früher gab es das nicht danke für die tipps!
danke für die tipps!
und das die eigenwerte ungenau rauskommen ist mir auch schon aufgefallen. bei großen matrizen ist mir das klar, aber mir ist das schon bei relativ kleinen passiert, was eigentlich unnötig ist.
den rest muss ich mir mal anschauen, früher gab es das nicht
 danke für die tipps!
danke für die tipps!und das die eigenwerte ungenau rauskommen ist mir auch schon aufgefallen. bei großen matrizen ist mir das klar, aber mir ist das schon bei relativ kleinen passiert, was eigentlich unnötig ist.
geht nur die (ich vermute mal dass sie es ist) 2-norm?
Jop. Gehen aber auch andere: norm[A, "norm"]. Also z.B.: norm[{{1,2},{3,4}},"Frobenius"]
bei großen matrizen ist mir das klar, aber mir ist das schon bei relativ kleinen passiert, was eigentlich unnötig ist.
Absolut. Verbessert sich aber kontinuierlich, lohnt hin und wieder mal paar Sachen zu testen.
fl0
Enthusiast
cool, das wird mir in zukunft öfter mal helfen 

BatzenXI
Neuling
- Mitglied seit
- 23.04.2011
- Beiträge
- 84
Ich brauch mal kurz Hilfe bei ner blöden C/C++ Aufgabe 
Und zwar ist die Aufgabenstellung wie folgt:
Aufgabe (1)
Es sollen alle Wände und die Deckeeines Raumes einmal in der gleichen Farbe gestrichen werden, Fenster und Türen müssen nicht berücksichtigt werden:
Eingabe:
Die 3 Raumgrößen (4, 3 , 2.5)
Ergiebigkeit der Farbe (in l/qm) (0.5)
Ausgabe:
Die zu streichende Fläche (in qm) (47)
Benötige farbmenge (in l) (23,5)
Die ist kein Problem, allerdings bei der 2. Aufgabe die darauf aufbaut hab ich nen Problem :/
(2)
Es gibt folgende Gebinde:
10l zu 35 Euro
5l zu 20 Euro
2l zu 9 Euro
1l zu 5 Euro
Das Programm soll die optimale Gebindekombination für minimalen Preis ermitteln.
Ausgabe:
Anzahl der benötigen Gebinde (2 zu 10, 0 zu 5, 2 zu 2, 0 zu 1)
Gesamtpreis (88)
Überlegen Sie sich Test und Grenzfälle sowie Möglichkeiten den Test zu vereinfachen.
(a,b1,c,d und farbe1,farbe2,farbe3,farbe4 sind Hilfsvariablen)
Momentan sieht das wie folgt aus:
// MALER1.cpp 29.02.2012
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
float b, l, h , fläche_wand1, fläche_wand2, fläche_decke, ergib_farbe, sum_fläche, farbe_ges, farbe_ges1, farbe1, farbe2, farbe3, farbe4, a = 0, b1 = 0, c = 0, d = 0, ges_preis;
cout << "Bitte geben Sie die Breite des Raumes ein: " << endl;
cin >> b;
cout << "Bitte geben Sie die Laenge des Raumes ein: " << endl;
cin >> l;
cout << "Bitte geben Sie die Hoehe des Raumes ein: " << endl;
cin >> h;
cout << "Bitte geben Sie die Ergiebigkeit der Farbe ein (l/qm): " << endl;
cin >> ergib_farbe;
fläche_wand1 = (b * h) * 2;
fläche_wand2 = (l * h) * 2;
fläche_decke = (b * l);
sum_fläche = fläche_wand1 + fläche_wand2 + fläche_decke;
farbe_ges = sum_fläche * ergib_farbe;
farbe_ges1 = farbe_ges;
farbe1 = 0;
farbe2 = 0;
farbe3 = 0;
farbe4 = 0;
for (a = 0; farbe1<=farbe_ges1; a++)
{
farbe1 = a * 10;
farbe_ges1 = farbe_ges1 - farbe1;
for (b1 = 0; farbe2 <= farbe_ges1; b1++)
{
farbe2 = b1 * 5;
farbe_ges1 = farbe_ges1 - farbe2;
for (c = 0; farbe3 <=farbe_ges1; c++)
{
farbe3= c * 2;
farbe_ges1 = farbe_ges1 - farbe3;
for(d = 0; farbe4 <=farbe_ges1; d++)
{
farbe4 = d * 1;
farbe_ges1 = farbe_ges1 - farbe4;
}
}
}
}
ges_preis = a * 35 + b1 * 20 + c * 9 + d * 5;
cout << "Die zu streichende Flaeche beträgt " << sum_fläche << " Quadratmeter." <<endl;
cout << "Sie benoetigen " << farbe_ges << " Liter Farbe." << endl << endl;
cout << "Sie benoetigt: " << "\t" << a << " 10 Liter" << endl;
cout << "\t" << "\t" << b1 << " 5 Liter" << endl;
cout << "\t" << "\t" << c << " 2 Liter" << endl;
cout << "\t" << "\t" << d << " 1 Liter" << endl;
cout << "Der Gesamtpreis beträgt " << ges_preis << " Euro." << endl;
return 0;
}

Und zwar ist die Aufgabenstellung wie folgt:
Aufgabe (1)
Es sollen alle Wände und die Deckeeines Raumes einmal in der gleichen Farbe gestrichen werden, Fenster und Türen müssen nicht berücksichtigt werden:
Eingabe:
Die 3 Raumgrößen (4, 3 , 2.5)
Ergiebigkeit der Farbe (in l/qm) (0.5)
Ausgabe:
Die zu streichende Fläche (in qm) (47)
Benötige farbmenge (in l) (23,5)
Die ist kein Problem, allerdings bei der 2. Aufgabe die darauf aufbaut hab ich nen Problem :/
(2)
Es gibt folgende Gebinde:
10l zu 35 Euro
5l zu 20 Euro
2l zu 9 Euro
1l zu 5 Euro
Das Programm soll die optimale Gebindekombination für minimalen Preis ermitteln.
Ausgabe:
Anzahl der benötigen Gebinde (2 zu 10, 0 zu 5, 2 zu 2, 0 zu 1)
Gesamtpreis (88)
Überlegen Sie sich Test und Grenzfälle sowie Möglichkeiten den Test zu vereinfachen.
(a,b1,c,d und farbe1,farbe2,farbe3,farbe4 sind Hilfsvariablen)
Momentan sieht das wie folgt aus:
// MALER1.cpp 29.02.2012
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
float b, l, h , fläche_wand1, fläche_wand2, fläche_decke, ergib_farbe, sum_fläche, farbe_ges, farbe_ges1, farbe1, farbe2, farbe3, farbe4, a = 0, b1 = 0, c = 0, d = 0, ges_preis;
cout << "Bitte geben Sie die Breite des Raumes ein: " << endl;
cin >> b;
cout << "Bitte geben Sie die Laenge des Raumes ein: " << endl;
cin >> l;
cout << "Bitte geben Sie die Hoehe des Raumes ein: " << endl;
cin >> h;
cout << "Bitte geben Sie die Ergiebigkeit der Farbe ein (l/qm): " << endl;
cin >> ergib_farbe;
fläche_wand1 = (b * h) * 2;
fläche_wand2 = (l * h) * 2;
fläche_decke = (b * l);
sum_fläche = fläche_wand1 + fläche_wand2 + fläche_decke;
farbe_ges = sum_fläche * ergib_farbe;
farbe_ges1 = farbe_ges;
farbe1 = 0;
farbe2 = 0;
farbe3 = 0;
farbe4 = 0;
for (a = 0; farbe1<=farbe_ges1; a++)
{
farbe1 = a * 10;
farbe_ges1 = farbe_ges1 - farbe1;
for (b1 = 0; farbe2 <= farbe_ges1; b1++)
{
farbe2 = b1 * 5;
farbe_ges1 = farbe_ges1 - farbe2;
for (c = 0; farbe3 <=farbe_ges1; c++)
{
farbe3= c * 2;
farbe_ges1 = farbe_ges1 - farbe3;
for(d = 0; farbe4 <=farbe_ges1; d++)
{
farbe4 = d * 1;
farbe_ges1 = farbe_ges1 - farbe4;
}
}
}
}
ges_preis = a * 35 + b1 * 20 + c * 9 + d * 5;
cout << "Die zu streichende Flaeche beträgt " << sum_fläche << " Quadratmeter." <<endl;
cout << "Sie benoetigen " << farbe_ges << " Liter Farbe." << endl << endl;
cout << "Sie benoetigt: " << "\t" << a << " 10 Liter" << endl;
cout << "\t" << "\t" << b1 << " 5 Liter" << endl;
cout << "\t" << "\t" << c << " 2 Liter" << endl;
cout << "\t" << "\t" << d << " 1 Liter" << endl;
cout << "Der Gesamtpreis beträgt " << ges_preis << " Euro." << endl;
return 0;
}
Zuletzt bearbeitet:
herrhannes
Enthusiast
- Mitglied seit
- 28.10.2006
- Beiträge
- 6.688
Also an sich ist das ja einfach, weil hier das größte Gebinde das billigste ist. Da ist es dann am einfachsten, immer per Modulo zur rechnen, wie wenn du Geld wechseln würdest: Erst die Großen und dann immer kleiner werden. Aufpassen musst du nur, dass du immer ganze Gebinde zahlen musst. Also wenn beim kleinsten ein Rest bleibt, zählt der wie ein Gebinde.
herrhannes
Enthusiast
- Mitglied seit
- 28.10.2006
- Beiträge
- 6.688
Also, um zu wissen, wieviel reinpasst nimmst du jeweils die Division deiner Menge durch die Gebindegröße. Als int, damit fällt die Zahl hinterm Komma weg.
Dann kannst du die entsprechende Variable setzen. Dann geht es mit der nächsten Größe weiter, die übrige Menge von vorher rechnest du über Modulo (%) aus.
Dann kannst du die entsprechende Variable setzen. Dann geht es mit der nächsten Größe weiter, die übrige Menge von vorher rechnest du über Modulo (%) aus.
herrhannes
Enthusiast
- Mitglied seit
- 28.10.2006
- Beiträge
- 6.688
Das ist kein Befehl, sondern ein Operator, der dir den Rest einer Division ausgibt. Schön wie in der Grundschule also 

Ich bräuchte mal Hilfe beim Ansatz für die partikuläre Lösung einer inhom. lin. DGL:
y´´´+y´´-y´-y = e^-x | oder = (x²+1)*e^x
Für den ersten Fall ist der Ansatz (laut Prof.) y=x²*A*e^(-x) und für den 2. Fall y=x*(Ax²+Bx+C)*e^x.
(A, B, C sind jeweils die zu bestimmenden Variablen)
Das kann ich auch fast nachvollziehen, nur ist mir nicht klar woher die beiden fett geschriebenen Faktoren kommen bzw. warum man die braucht.
Kann mir das jemand erklären?
danke!
y´´´+y´´-y´-y = e^-x | oder = (x²+1)*e^x
Für den ersten Fall ist der Ansatz (laut Prof.) y=x²*A*e^(-x) und für den 2. Fall y=x*(Ax²+Bx+C)*e^x.
(A, B, C sind jeweils die zu bestimmenden Variablen)
Das kann ich auch fast nachvollziehen, nur ist mir nicht klar woher die beiden fett geschriebenen Faktoren kommen bzw. warum man die braucht.
Kann mir das jemand erklären?
danke!
Zuletzt bearbeitet:
Folgende Aufgabe:

Gegeben habe ich laut der Aufgabe ja fV (12000Hz) da Jagger ab da nichts mehr hört, c ist auch bekannt da Schallgeschwindigkeit (343 m/sec) aber fehlt mir da nicht noch eine Angabe? Ich muss an v kommen, brauche doch aber dafür doch noch die Frequenz mit der die Hupe den Hupton aussendet, oder nicht?

Gegeben habe ich laut der Aufgabe ja fV (12000Hz) da Jagger ab da nichts mehr hört, c ist auch bekannt da Schallgeschwindigkeit (343 m/sec) aber fehlt mir da nicht noch eine Angabe? Ich muss an v kommen, brauche doch aber dafür doch noch die Frequenz mit der die Hupe den Hupton aussendet, oder nicht?

TheWarrior
Enthusiast
- Mitglied seit
- 15.11.2003
- Beiträge
- 384
Setz doch einfach alle üblichen Verdächtigen (50km/h, 30km/h, Schrittgeschwindigkeit) ein und guck dir an, was du als Ergebnis bekommst.
Ähnliche Themen
- Antworten
- 0
- Aufrufe
- 824