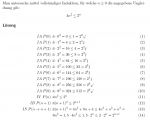jetzt steh ich seit 4h woanders an -.-
IA 1/1^2 = 1 <= 1 = 2/(1(1+1))
IV 1/n^2<= 2/(n(n+1))
IB 1/(n+1)^2<= 2/((n+1)(n+2))
IS 1/(n+1)^2 <= ... <= 2/((n+1)(n+2))
egal was ich veranstalte ich bekomme 1/(n+1)^2 einfach nicht so umgeformt dass <= 2/((n+1)(n+2)) rauskommt
du sollst auch nicht umformen. wenn man das umformen könnte würde stets gleichheit gelten. du sollst zeigen dass die ungleichung gilt. und das geht so:
zu zeigen ist was? 1/(n^2) <= 2/n(n+1)? das ist also die induktionshypothese. da alles größer null ist kann man das äquivalent umformen zu n(n+1) <= 2*n^2.
nach dem induktionsschritt sieht das ganze so aus
(n+1)(n+2) <= 2*n^2+4n+2.
fangen wir mal auf der linken seite an und lösen die rechte klammer auf
(n+1)(n+2) = n(n+1) + 2(n+1)
hier erkennt man direkt die induktionshypothese und kann sie einsetzen (und das ist der "trick" bei jeeeeeeeder induktion. auf einer seite anfangen und versuchen nach dem induktionsschritt wieder die induktionshypothese rauszuschreiben), das ergibt:
n(n+1) + 2(n+1) <= 2*n^2 +2n+2
und das kann man ruhigem gewissens nach oben abschätzen indem man sagt
2*n^2 +2n+2 <= 2*n^2 +4n+2
also hat man ingesamt die aussage für n+1 dastehen
(n+1)(n+2)<=2*n^2 +4n+2
wenn du noch fragen zur induktion hast, kannst du die gerne stellen. wenn du noch fragen zur konvergenz von reihen hast, kannst du die auch gerne stellen. ich werd dir die beweise nachreichen, aber im moment hab daheim keine zeit zu suchen. das heir schreibe ich von unterwegs, da habe ich aber die ana1 unterlagen natürlich nicht dabei.
---------- Post added at 21:10 ---------- Previous post was at 20:49 ----------
Dann muss man bei der Überprüfung der Ränder halt auf was anderes zurückgreifen als das Quotienten oder Wurzelkriterium. Leibniz, abschätzen etc., gibt ja genug Möglichkeiten.
Ich habe nur wiedergegeben was ich gelernt habe, und bei uns gehörte beim Bestimmen des Konvergenzradius das Prüfen der Ränder (eben die Fälle wo das Quotkrit keine Aussage macht) immer dazu. Das wegzulassen führte bei uns zu Punktabzug.
Mit der absoluten Konvergenz habe ich mich nur an das gehalten, was im Bronstein steht und für mich auch sinnvoll klingt. Dort steht: "Eine Potenzreihe konvergiert ...(andere Möglichkeiten wie ein festes x oder alle x aus R)..., oder es gibt eine Zahl p>0, den Konvergenzradius, so dass die Reihe für |x-x0|< p absolut konvergiert...". Das Konvergenz aus absoluter Konvergenz folgt ist klar, hab ich oben nicht so deutlich ausgedrückt.
Vielleicht ist symetrisch das falsche Wort. Ich wollte nur deutlich machen, dass man eben zwischen den Werten von x, die eben ein Intervall wie [0|2) annehmen können, und dem Konvergenzradius unterscheiden muss. Der Radius ist ja nur eine Zahl und in diesem Bereich konvergiert es. Mit symetrisch meinte ich eben, dass x-x0 dann Werte im Bereich von -p bis p annehmen kann.
und noch ein drittes mal, mit dem wurzel- oder quotientenkriterium überprüft man ob eine reihe konvergiert. dazu muss gelten dass das wurzelkonstrukt oder der quotient den man dazu aus der ursprünglichen reihe bildet echt kleiner 1 sein muss. das steht sogar hier
Quotientenkriterium und hier
Wurzelkriterium richtig. es gibt dort keine ränder, es gibt dort keine randwerte, es gibt dort nichts was man zusätzlich überprüfen müsste. es gibt nichts zu tun, ausser den quotienten zu bilden und zu schauen ob er echt kleiner1 ist. oder den wurzelausdruck. man kann auch absolut nichts festellen, ausser ob die reihe konvergiert. nicht wo, nicht wann. nur ob.
und sieh bitte nochmal genau nach was im bronstein steht und ob du es auch nicht vielleicht aus dem zusammenhang gerissen hast. absolute konvergenz bedeutet der betrag der reihe konvergiert und nichts anderes. was man natürlich sagen kann ist (was du auch zitiert hast), wenn eine potenzreihe konvergiert, also ein R existiert, dann konvergiert die reihe absolut für alle |x-x_0|< R. auch hier steht echt kleiner R. das einzige was halt ist, dass man randpunkte wieder händisch untersuchen muss. du hast geschrieben, wenn das quotientenkrit <= 1 ist, ists konvergent und wenns < 1 ist absolut. aber das stimmt nicht. wenn man einen randwert einsetzt und es konvergiert, dann konvergiert es halt. wenn man einen randpunkt einsetzt und es divergiert, dann divergiert es halt. wenn man einen randpunkt in die "absolute" reihe einsetzt und es konvergiert, dann konvergiert es halt absolut. und wenn man einen randwert in die "absolute" reihe einsetzt und es divergiert, dann divergiert es dort halt.